lunes, 29 de febrero de 2016
sábado, 27 de febrero de 2016
Límites: Indeterminacion infinito entre infinito
Límite inf/inf
1º forma: Con la Regla de L`Hôpital: derivamos tantas veces como sea necesario hasta que el límite da un número
2º forma: Parte dominante: Nos quedamos con la x de mayor potencia y su coeficiente, en el numerador y en el denominador. Luego simplificamos y sustituimos la x por el límite.
Si el grado del numerador es mayor que el del denominador, el resultado va a ser infnito.
Cuando el numerador y el denominador tienen el mismo grado, el resultado va a ser un número
Cuando el grado del numerador es menor que el del denominador, el resultado va a ser cero.
Derivadas varias: x, 1/x, raíz, ln, e^x, coseno
Derivadas de un número, de x, de 1/x, de una raíz, del logaritmo neperiano, de e^x y del coseno,
Límites: Indeterminación 0/0
Límite de una función que da como resultado 0/0, que es una indeterminación.
Hay 3 formas de resolverla:
1. Factorizamos el numerador y el denominador, simplificamos y sustituimos el valor de x por el valor del límite.
2. En caso de suma o resta de raíces: Multiplicamos por el conjugado y obtenemos el producto notable a^2-b^2
2. Regla de L'Hôpital: (también válida para inf/inf) derivamos el numerador y el denominador, tantas veces como sea necesario hasta que nos de un número.
viernes, 26 de febrero de 2016
jueves, 25 de febrero de 2016
Teoría de Conjuntos
Un conjunto es una agrupación cualquiera de objetos con una característica específica que permite determinar con certeza si un objeto pertenece o no a la agrupación
Los objetos que forman parte del conjunto se denominan elementos. Si un elemento forma parte de un conjunto se dice que el elemento pertenece (E) al conjunto. Si el elemento no forma parte del conjunto, se dice que no pertenece (/E) al conjunto.
Los conjuntos pueden representarse entre llaves o en diagramas y se designan por letras mayúsculas A, B, C,..., y los elementos de un conjunto por letras minúsculas a, b, c,...
El número de elementos que forman un conjunto, A, se escribirá n(A) y se llama cardinal de A.
Supongamos que P y Q son dos conjuntos. Se dice que P es un subconjunto de Q si cada elemento de P está incluido en Q y se representa por:
Si P es un subconjunto de Q , pero no igual a este lo escribiremos:
Álgebra de Conjuntos
Unión. La unión de dos conjuntos A y B es el conjunto A ∪ B que contiene cada elemento que está por lo menos en uno de ellos.
Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B.
Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.
Complemento. El complemento de un conjunto A es el conjunto A∁ que contiene todos los elementos (respecto de algún conjunto referencial) que no pertenecen a A.
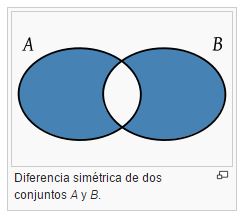
Diferencia simétrica La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer elemento a pertenece a A y su segundo elemento b pertenece a B.
Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B.
Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.
Complemento. El complemento de un conjunto A es el conjunto A∁ que contiene todos los elementos (respecto de algún conjunto referencial) que no pertenecen a A.
Diferencia simétrica La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer elemento a pertenece a A y su segundo elemento b pertenece a B.
Suscribirse a:
Comentarios (Atom)